METODE TERBUKA:
ITERASI
SATU TITIK SEDERHANA, NEWTON RAPHSON
MAKALAH
Disusun
untuk Memenuhi Salah Satu Tugas Mata Kuliah Fisika Komputasi
Dosen
Pengampu:
Winda
Setya, M.Sc.
Disusun
oleh:
Kelompok
3
Novia
Melinda 1182070043
Nursalmah
Faturrahmah 1182070046
Vidya
Astuti 1182070067
Semester
6B
PROGRAM
STUDI PENDIDIKAN FISIKA JURUSAN PENDIDIKAN MIPA
FAKULTAS
TARBIYAH DAN KEGURUAN
UIN
SUNAN GUNUNG DJATI
BANDUNG
2021
KATA PENGANTAR
Puji dan syukur kami panjatkan kepada
Tuhan Yang Maha Esa atas berkat, rahmat, dan karunia-Nya sehingga kami dapat
menyelesaikan makalah “Metode Terbuka: Iterasi Satu Titik Sederhana, Newton-Raphson”
tepat pada waktunya. Shalawat serta salam kami sampaikan bagi Nabi Muhammad
SAW.
Adapun maksud dan tujuan dari
penyusunan makalah ini adalah untuk memenuhi salah satu tugas yang diberikan
oleh dosen pada mata kuliah Fisika Komputasi. Proses penyusunan makalah ini tentunya
melalui berbagai hambatan, namun berkat dukungan dari berbagai pihak kami dapat
menyelesaikan tugas ini dengan baik. Oleh karena itu, kami menyampaikan terima
kasih kepada berbagai pihak yang telah membantu terselesaikannya tugas makalah
ini.
Bandung, Maret 2021
Penulis
DAFTAR ISI
A. Metode
Iterasi Satu Titik Sederhana
D. Penentuan Kriteria Berhenti
Iterasi
E. Jebakan Pada Metode
Newton-Raphson
BAB I
PENDAHULUAN
A. Latar Belakang Masalah
Metode numerik merupakan metode yang menggunakan operasi hitung berupa operasi tambah, kurang, kali, dan bagi untuk menyelesaikan permasalahan-permasalahan yang diformulasikan secara matematis. Metode numerik memiliki ciri yaitu solusi yang didapatkan berupa angka, hanya memperoleh solusi yang menghampiri atau mendekati solusi sejati sehingga solusi numerik dimanakan solusi hampiran. Solusi hampiran memiliki selisih dengan solusi sejati, selisih ini disebut dengan galat atau error ().
Metode numerik
bertujuan untuk memudahkan penyelesaian permasalahan yang membutuhkan
penjabaran panjang dan rumit jika menggunakan metode analitik. Salah satu
contohnya adalah menentukan akar-akar persamaan, jika diselesaikan menggunakan
metode analitik maka penjabarannya sangat panjang sehingga tidak efisien. Untuk
itu menetukan akar-akar persamaan dapat dilakukan menggunakan metode numerik
yang disajikan dalam bentuk algoritma yang akan melakukan perhitungan secara
iterasi sehingga didapatkan hasil yang mendekati solusi sejati. Metode terbuka
merupakan metode numerik yang digunakan untuk mencari akar-akar persamaan.
Metode terbuka meliputi metoda iterasi satu titik
sederhana, metoda Newton-Raphson dan metoda Secant.
B. Rumusan Masalah
1.
Bagaimana metode iterasi satu titik sederhana?
2.
Bagaimana metode
dua grafik?
3.
Bagaimana metode Newton-Raphson?
4.
Bagaimana penentuan kriteria berhenti iterasi?
5.
Bagaimana jebakan pada metode Newton-Raphson?
C. Tujuan
1.
Mengetahui bagaimana metode iterasi satu titik sederhana.
2.
Mengetahui
bagaimana metode dua grafik.
3.
Mengetahui bagaimana metode Newton-Raphson.
4.
Mengetahui bagaimana penentuan kriteria berhenti iterasi.
5.
Memahami bagaimana jebakan pada metode Newton-Raphson.
BAB II
PEMBAHASAN
Metode terbuka
adalah metode yang menggunakan satu, atau dua tebakan awal yang tidak perlu
mengurung akar atau tidak memerlukan rentang sejumlah nilai
A.
Metode Iterasi Satu Titik Sederhana
Teknik
menentukan hampiran akar persamaan secara umum tergantung pada dugaan nilai
awal yang mengapit nilai akar. Dalam beberapa kasus hal ini sulit dilakukan,
sehingga diperlukan suatu metode yang tidak memerlukan informasi awal. Salah
satu metode yang demikian adalah metode iterasi satu titik sederhana
Metode
iterasi satu titik sederhana adalah metode yang memisahkan x dengan yang lain
sehingga diperoleh
Gambar 1. Ilustrasi metode iterasi satu titik sederhana
Metode
ini kadang – kadang dinamakan juga metoda langsung atau metoda substitusi
beruntun. Kesederhanaan metoda ini karena pembentukan prosedur iterasinya mudah
dibentuk dalam bentuk persamaan (1.1) berikut.
Persamaan
tersebut diperoleh dari f(x) = 0 yang diubah menjadi bentuk persamaan
(1.1). Setelah itu ditentukan tebakan awal ![]()
Metode iterasi satu titik bisa konvergen
tergantung dari tebakan awal dan bagaimana perilaku fungsi. Contoh:
Fungsi dipisahkan dan dinyatakn dalam bentuk
persamaan
Dengan tebakan awal, iterasi menghasilkan
Tabel 1. Hasil perhitungan dengan metode Iterasi Satu Titik Sederhana
Kesalahan relatif
kira-kira 0,5 hingga 0,6 dari kesalahan iterasi sebelumnya, ini disebut
konvergensi linear.
Algoritma Metode Iterasi Satu Titik Sederhana
1. Definisikan f(x) dan g(x)
2. Tentukan nilai
toleransi e dan iterasi masimum (N)
3. Tentukan tebakan
awal
4. Untuk iterasi i=1 s/d N
atau
5. Akar persamaan
adalah x terakhir yang diperoleh
Contoh pengaplikasian metode iterasi satu
titik sederhana dengan bantuan Matlab:
Soal: Dengan menggunakan
metoda iterasi satu titik sederhana dan bantuan perangkat lunak Matlab,
tentukan akar dari persamaan berikut
Penyelesaian:
clc
clear all
close all
close all hidden
%
[x,fval,exitflag,output] = fzero(@(x) (x^4) - (8.50*x^3) -
(35.50*x^2) + (465*x) - 1000 ,3)
Hasil program
x =
3.8823
fval =
0
exitflag =
1
output =
intervaliterations : 8
iterations : 7
funcCount : 24
algorithm : ‘bisection,
interpolation’
message : ‘Zero found in the interval [2.04,
3.96]
Akar
dari persamaan di atas adalah 3.8823 yang diperoleh pada iterasi ke-7.
B.
Metode Dua Grafik
Langkah-langkah penyelesaian Newton-Raphson
secara grafis (lihat gambar 2):
a.
Tentukan sembarang titik ![]()
![]()
b.
Buat garis singgung pada![]() sehingga
memotong sumbu
sehingga
memotong sumbu ![]()
c.
Dari![]() tarik garis keatas sehingga memotong kurva
fungsi di
tarik garis keatas sehingga memotong kurva
fungsi di ![]()
d.
Buat garis singgung pada![]() sehingga
memotong sumbu
sehingga
memotong sumbu
e.
Dari x3
f. Demikian seterusnya sampai mendekati titik x,
dimana titik x inilah salah satu akar dari persamaan.
Gambar
2. Metode Newton-Raphson
Pernyataan masalah : pisahkan persamaan
Solusi : tuliskan kembali persamaan sebagai
Didapatkan perhitungan yang disajikan pada tabel 1 dibawah ini
Tabel 2. Hasil
perhitungan dengan metode grafik 2 kurva
|
|
|
|
|
0,0 |
0,0 |
1,000 |
|
0,2 |
0,2 |
0,819 |
|
0,4 |
0,4 |
0,670 |
|
0,6 |
0,6 |
0,549 |
|
0,8 |
0,8 |
0,449 |
|
1,0 |
1,0 |
0,368 |
Titik-titik ini telah digambarkan pada gambar
berikut.
Gambar 3. Dua
metode grafik alternative untuk menentukan akar dari
Pada gambar 3a terlihat bahwa akar berada pada titik dimana ia memotong sumbu x. Gambar 1b adalah akar perpontongan dai fungsi – fungsi komponen. Harga-harga x yang bersesuaian dengan perpotongan kedua fungsi dinyatakan oleh akar f(x) =0
Perpotongan dari kedua kurva tampak pada taksiran
akar x=0,57
Pada
gambar 4 di atas grafik (a) dan (c) dinamakan pola monoton, sedangkan (b) dan
(d) dinamakan osilasi atau pola spiral. Perhatikan bahwa konvergensi terjadi
bila [g'(x)}<1
C. Metode Newton-Raphson
Metode
Newton-Raphson merupakan salah satu metode yang paling banyak digunakan dalam
terapan sains dan rekayasa seperti untuk mencari akar-akar persamaan non-linear
karena konvergensinya cepat dibanding metode lainnya. Metode ini diperkenalkan
oleh Joseph Raphson dan Isaac Newton, serta termasuk kedalam metode terbuka
dalam penyelesaian persamaan
Kurva fungsi yang bersangkutan dalam
metode Newton-Raphson dihampiri
dengan garis singgung kurva dititik yang sudah diperoleh. Kekonvergenan metode ini bersifat kuadratik (derajat kekonvergenannya 2) ke akar sederhana. Untuk akar ganda,
metode ini mempunyai derajat kekonvergenan linier, dan dapat ditingkatkan
menjadi kuadratik dengan memodifikasi rumus iterasinya, namun modifikasi rumus
iterasi metode Newton-Raphson memerlukan
informasi derajat akar atau perhitungan turunan yang lebih tinggi (untuk
mengetahui derajat akarnya).
Penurunan
persamaan pada metode Newton-Raphson memiliki dua pendekatan yang dapat
digunakan
1. Penurunan
metode Newton-Raphson secara geometri
Gambar
5. Analisis geometri metode Newton-Raphson
Source:
Buku Metode Numerik
Berdasarkan Gambar 5, gradien garis singgung di
Atau
Sehingga prosedur iterasi metode
Newton-Raphson dengan pengeksplisistan xr+1
2. Penurunan
metode Newton-Raphson dengan bantuan deret Taylor
Deret Taylor didefinisikan sebagai
suatu fungsi f dan semua turunannya pada interval tertutup [a, b], yaitu:
Apabila deret ini
dipotong sampai dengan orde ke-2, maka deret Taylor menjadi
dengan 1! = 1, sehingga
untuk uraian
Akar persamaan diperoleh jika![]() =0, dengan demikian prosedur iterasi yang
merupakan iterasi Newton-Raphson adalah
=0, dengan demikian prosedur iterasi yang
merupakan iterasi Newton-Raphson adalah
Iterasi Newton-Raphson berhenti apabila
atau secara relatif
Algoritma Metode
Newton-Raphson,
1.
Definisikan fungsi f(x)
2.
Tentukan toleransi error
dan iterasi maksimum.
3.
Tentukan nilai
pendekatan awal (x0)
4.
Hitung f(x0)
5.
Untuk iterasi
Hitung f(Xr)
6.
Akar persamaan adalah nilai Xrn
Adapun langkah-langkah penentuan akar dari suatu
persamaan dengan metode Newton-Raphson adalah sebagai berikut
1. Tentukan
taksiran awal akar untuk fungsi f(x)
2. Tentukan
turunan pertama dari fungsi f(x)
3. Lakukan
evaluasi f(x)
4. Hitung
pendekatan akar yang baru dari fungsi f(x)
5. Periksa
kesalahan relatif
a. Jika
kesalahan relatif
b. Jika
kesalahan relatif
Kriteria konvergensi metode
Newton-Raphson, metode ini merupakan metode terbuka yang bentuk umum lelarannya
yaitu,
Maka, untuk metode
Newton-Raphson sebagai berikut.
Syarat agar lelaran konvergen adalah
Karena itu, metode Newton-Raphson akan konvergen jika
Contoh pengaplikasian metode Newton-Raphson
Soal:
Dengan menggunakan metode Newton-Raphson dan bantuan perangkat lunak Matlab,
tentukan akar dari persamaan berikut
Penyelesaian:
Script
Matlab
clc
clear all
close all
%
disp(‘Metoda Newton Raphson’);
disp(‘======================’);
x = input(‘Nilai Tebakan Awal : ‘);
eps = input(‘Nilai Ketelitian : ‘);
itemax = input(‘Jumlah Iterasi Maksimum : ‘);
alfa = x;
disp (‘ ‘);
disp (‘Proses Iterasi’)
disp (‘======================’)
xlama = x;
tic
for i = 1:1:itemax
if ft(xlama) == 0
break;
else
xbaru = xlama -
(fn(xlama,alfa)/ft(xlama));
end
disp ([‘Iterasi ke
‘,num2str(i),’,’,’ akar :
‘,num2str(xbaru)])
if
abs((xbaru-xlama)/xbaru) <= eps
break;
end
xlama = xbaru;
end
salah = abs((xbaru-xlama)/xbaru);
disp (‘ ‘)
disp ([‘Nilai Akar : ‘,num2str(xbaru)])
disp ([‘Jumlah Iterasi : ‘,num2str(i)])
disp ([‘Kesalahan : ‘,num2str(salah)])
function f = fn(x,alfa);
f = x^4 - 8.5000*x^3 - 35.5000*x^2 + 465.0000*x - 1000.0000;
function f = ft(x);
f = 4*x^3 - 25.5000*x^2 - 71.0000*x + 465.0000;
Hasil Program
Metoda Newton Raphson
======================
Nilai Tebakan Awal : 3.0000
Nilai Ketelitian : 0.00001
Jumlah Iterasi Maksimum : 100
Proses Iterasi
======================
Iterasi ke 1, akar : 3.5594
Iterasi ke 2, akar : 3.81
Iterasi ke 3, akar : 3.8771
Iterasi ke 4, akar : 3.8823
Iterasi ke 5, akar : 3.8823
Nilai Akar : 3.8823
Jumlah Iterasi : 5
Kesalahan : 7.7129e-06
Akar dari persamaan diatas adalah 3.8823
yang diperoleh pada iterasi ke 5 dengan tingkat ketelitian kecil dari 0.0010 %.
D.
Penentuan Kriteria Berhenti Iterasi
Penetuan
kriteria berhenti iterasi pada metode Newton Raphson ditentukan berdasarkan
taksiran kesalahan yang tidak ditentukan oleh pengetahuan tentang akar itu
sebelumnya
Iterasi Newton-Raphson berhenti apabila
Contoh,
menetukan akar persamaan dari fungsi
Tabel
2. Hasil Iterasi Newton-Raphson
Source:
|
i |
|
|
|
0 |
0.500000 |
- |
|
1 |
0.618976 |
0.118976 |
|
2 |
0.605444 |
0.013532 |
|
3 |
0.605266 |
0.000177 |
|
4 |
0.605267 |
0.000000 |
Berdasarkan Tabel 2 diperoleh hampiran
akar
E.
Jebakan Pada Metode Newton-Raphson
Metode Newton-Raphson tidak menggunakan prinsip
penggunaan akar lagi, akibatnya metode Newton-Raphson tidak dijamin lagi
kekonvergenannya
Pernyataan masalah: tentukan akar positif dari
Solusi
Tabel 3. Hasil perhitungan untuk jebakan pada
metode Newton-Raphson
|
Iterasi |
|
|
0 |
0,5 |
|
1 |
51,65 |
|
2 |
46,485 |
|
3 |
41,8365 |
|
4 |
37,65285 |
|
5 |
33,887565 |
|
… |
… |
|
|
1,000000000 |
Setelah taksiran pertama, ia akan konvergen
pada akar sebenarnya, yakni 1, tapi dengan kelajuan yang sangat perlahan.
Disamping konvergen yang perlahan yang di sebabkan sifat bawaan fungsi,
kesukaran lain timbul, seperti diperlihatkan pada gambar dibawah ini.
Gambar 6. Empat kasus dimana metode Newton-Raphson memperlihatkan konvergen yang kurang baik
Gambar
6a memperlihatkan kasus dimana sebuah titik belok, yakni
Gambar 6b memperlihatkan kecenderungan dan teknik
Newton-Raphson untuk berisolasi disekitar harga maksimal dan minimal setempat.
Osilasi yanyg demikian bisa tertahan atau seperti dalam gambar 3b, sebuah
kemiringan yang mendekati ol dicapai dimana solusi ditempatkan jauh dari daerah
yang diinginkan.
Gambar 6c memperlihatkan bagaimana sebuah tebakan awal yang
mendekati suatu akar dapat meloncar kesuatu lokasi jauh dari beberapa akar.
Kecenderungan menjauh dari daerah yanyg diinginkan disebabkan ditemukannya
nilai kemiringan yang mendekati nol. Tentunya harga kemiringan nol yakni
F. Contoh Soal
Soal : Metode Iterasi Titik Tetap
Tentukan akar dari fungsi
Penyelesaian :
1)
Buka aplikasi Matlab, maka akan muncul kotak logo seperti berikut
3)
Setelah
itu akan tampil kolom editor kemudian isikan Source Code sebagai berikut :
tic;%awal program
clc;clear;%membersihkan commond window
Xn=1;%deklarasi variabel dan inisialisasi Xn=1
eps=10^(-6);%galat toleransi
galat=1;%inisialisasi nilai galat=1
k=1;%deklarasi variabel dan inisialisasi k=0
while
galat>eps;
Xn1=sqrt(4*Xn+log(Xn));
FXn=Xn1.^2-4*Xn1-log(Xn1);
Xn=Xn1;
galat=abs(FXn);
k=k+1;
end
disp('Akar
dari fungsi X^2-4*X-ln(X)dengan metode iterasi titik tetap');
%menampilkan kalimat 'Akar dari fungsi
X^2-4*Xln(X)dengan metode iterasi titik tetap'
disp('-------------------------------------------------
--------------');
%menampilkan simbol '--------------------------------'
fprintf('Akar Hampiran = %10.8f\n',Xn1);
%menampilkan kalimat 'Akar Hampiran = ' serta nilai
pada Xn1 dengan 10 space dan 8 angka dibelakang koma
fprintf('Nilai fungsi = %10.8f\n',FXn);
%menampilkan kalimat 'Nilai fungsi = ' serta nilai
pada FXn dengan 10 space dan 8 angka dibelakang koma
fprintf('Akar fungsi abs = %10.8f\n',galat);
%menampilkan kalimat 'Akar fungsi abs = ' serta
nilai pada galat dengan 10 space dan 8 angka dibelakang koma
fprintf('banyak iterasi = %4.0f\n',k);
%menampilkan kalimat 'banyak iterasi =' serta nilai
pada k dengan 4 space dan 0 angka dibelakang koma
fprintf('selang waktu konvergen = %10.8f\n',toc);
%menampilkan kalimat 'selang waktu konvergen ='
serta nilai pada toc dengan 10 space dan 8 angka dibelakang koma
4)
Setelah
itu klik run atau juga bisa di copy ke command windows dan di enter
5)
Maka
akan didapat hasil
Jadi
dari output software Matlab di atas ditemukan akar persamaannya adalah 4.33826293
dengan 26 kali iterasi dan selang waktu konvergen adalah 0.01987751 detik.
Soal:
Metode Newton-Raphson Menggunakan Matlab
Persamaan keadaan van der Waals, perpanjangan sederhana dari hukum gas ideal yang ditemukan pada tahun 1873 oleh fisikawan Belanda Johanes Diderik van der Waals, adalah
|
Gas |
a |
b |
|
|
1.36 |
0.0318 |
|
|
3.78 |
0.0441 |
|
|
6.71 |
0.0564 |
Penyelesaian:
1) Tentukan fungsi tiap gas
Fungsi dari persamaan
Van der Waals sebagai berikut.
Kedua ruas dikalikan
dengan V2
Berikut ini fungsi tiap gas berdasarkan tabel diatas.
Berikut ini trurunan
pertama dari fungsi tiap gas berdasarkan tabel diatas.
3) Buka Matlab 2013a hingga muncul tampilan berikut
4) Klik New Script pada bagian pojok kiri atas hingga muncul tampilan berikut
5) Simpan script tiap fungsi dan turunannya sebagai berikut
· Fungsi gas
function y=fungsigas(v)
y=v^3-(22.4178*v^2)+(1.36*v)-0.0432;
end
· Diferensial fungsi gas
function y=fungsigas_diff(v)
y=(3*v^2)-(44.8356*v)+1.36;
end
· Fungsi gas
function y=fungsigas2(v)
y=v^3-(22.4301*v^2)+(3.78*v)-0.1550;
end
· Diferensial fungsi gas
function y=fungsigas2_diff(v)
y=(3*v^2)-(44.8602*v)+3.78;
end
· Fungsi gas
function y=fungsigas3(v)
y=v^3-(22.4424*v^2)+(6.71*v)-0.3784;
end
· Diferensial fungsi gas
function y=fungsigas3_diff(v)
y=(3*v^2)-(44.8848*v)+6.71;
end
6) Simpan script berikut dengan nama “Newton.m”
clear
clc
disp('Metode Newton-Raphson');
disp('Tekan enter untuk lanjut');
pause
f=input('Fungsi f:');
f_diff=input('Turunan fungsi f:');
x1=input('Masukan nilai awal:');
imax=input('Masukan iterasi maksimal:');
galat1=input('Masukan galat toleransi:');
iter=0;
fprintf('\n Iterasi Akar f(Akar) Galat\n');
for k=1:imax
iter=iter+1;
x2=x1-(feval(f,x1)/feval(f_diff,x1));
galat=abs((x2-x1)/x2);
x1=x2;
y=feval(f,x1);
fprintf('%10.0f %6.10f %6.10f %6.10f\n',[iter;x1;y;galat])
if (galat<galat1 || (iter>imax)),break,end
end
fprintf('Akarnya adalah = %6.10f\n',x1)
7) Pada script “Newton.m” klik run yang terdapat dibagian atas hingga muncul tampilan sebagai berikut
Dapat juga dengan mengcopy-paste script ke bagian command window lalu tekan enter.
“selalu tekan enter untuk lanjut ke langkah berikutnya”
8) Masukan fungsi sesuai perintah dengan format ‘namafungsi’
9) Masukan nilai awal, iterasi maksimum, dan galat toleransi
10) Akan muncul hasil sebagai berikut
Hasil iterasi
BAB III
PENUTUP
Kesimpulan
Metode terbuka adalah
metode yang menggunakan satu, atau dua tebakan awal yang tidak perlu mengurung
akar atau tidak memerlukan rentang sejumlah nilai. Metode terbuka terdiri dari
metode iterasi satu titik sederhana, metode Newton-Raphson dan metode Secant.
Metode iterasi satu
titik sederhana adalah metode yang memisahkan x dengan yang lain sehingga
diperoleh
Metode Newton-Raphson
merupakan metode yang memiliki konvergensi cepat dibanding metode lainnya
sehingga paling banyak digunakan dalam terapan sains dan rekayasa. Metode ini
memiliki dua pendekatan dalam penurunan persamaannya, yaitu penurunan secara
geometri dan penurunan dengan bantuan deret Taylor. Penetuan kriteria berhenti
iterasi pada metode Newton Raphson ditentukan berdasarkan taksiran kesalahan
terhadap nilai toleransi yang telah ditentukan. Iterasi akan berhenti ketika
nilai taksiran kesalahan lebih kecil dan mendekati nilai toleransi.
Jebakan pada metode
Newton-Raphson yaitu kekonvergenan yang lambat karena
sifat alami dari fungsinya, iterasi yang dimulai pada
DAFTAR PUSTAKA
Afrianiita,
R., & Laksono, H. D. (2015). Metoda Numerik dengan Matlab. Padang:
(LPTIK) Universitas Andalas.
Afrianita, R. &. (2015). Metode Numerik
dengan Matlab. Padang: LPTIK Universitas Andalas.
Atmika, I. (2016). Diktat Mata Kuliah: Metode
Numerik. Jurusan Teknik Mesin Universitas Udayana.
Chapra, S. C. (1989). Metode Numerik Edisi
Ke-2. Jakarta: Erlangga.
Hutagalung, S. N. (2017). Pemahaman Metode Numerik
(studi Kasus Metode Newton-Raphson) Menggunakan Pemrogaman Matlab. Jurnal
teknologi Informasi. 1(1), 95-100.
Mahmul, M. K. (2017). Modifikasi Metode
Newton-Raphson untuk Mencari Solusi Persamaan Linear dan Nonlinear. Buletin
Ilmiah Mat. Stat. dan Terapannya (Bimaster). 6(2), 69-76.
Munir, R. (2017). Metode Numerik Sebagai
Algoritma Komputasi. Surabaya: Politeknik Elektronika Negeri
Surabaya-ITS.
Prastiyo, Y. (2018). ANALISA NUMERIK KEKUATAN
RANGKA PADA PROTOTYPE ELEVATOR PABRIK KELAPA SAWIT (SKRIPSI). Medan:
FAKULTAS TEKNIK UNIVERSITAS MUHAMMADIYAH SUMATERA UTARA.
Ritonga, J. &. (2019). Perbandingan Kecepatan
Konvergensi Akar Persamaan Non Linier Metode Titik Tetap dengan Metode
Newton-Raphson Menggunakan Matlab. Informasi (Jurnal Informatika dan
Sistem Informasi). 11(2), 51-64.
Ritonga, J. S. (2019). PERBANDINGAN KECEPATAN
KONVERGENSI AKAR PERSAMAAN NON LINIER METODE TITIK TETAP DENGAN METODE NEWTON
RAPHSON MENGGUNAKAN MATLAB. INFORMASI (Jurnal Informatika dan Sistem
Informasi), 51-64.
Sasongko, S. B. (2010). METODE NUMERIK DENGAN
SCILAB. Yogyakarta: C.V Andi Offset .
Subakti, I. (2004). Metode Numerik Edisi
Jurusan T. Informatika ITS. Surabaya: Institut Teknologi Sepuluh
November.
Susila, I. N. (1993). Dasar-Dasat Metode
Numerik. Bandung: Departemen Pendidikan dan Kebudayaan Direktorat
Jenderak Pendidikan Tinggi Proyek Pembinaan Tenaga Kependidikan Pendidikan
TInggi.
Triatmojo, B. (1995). Metode Numerik.
Yogyakarta: Beta Offset.
Zulkarnain, &. J. (2020). Solusi Numerik
Logika Fisika Berbasis Matlab Algoritm. Malang: Ahlimedia Press.




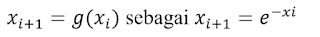








































0 Komentar